第1回:セットベースデザイン シミュレーションの原点

セットベースデザインを「科学、シミュレーション、設計」の3回シリーズで解説します。
第1回目では、工学は自然という大地から誕生した科学という大樹の一本のしっかりした枝であること、逆にいえば地中にしっかり根を張った科学という思考がルーツであることを確認することの重要性についてまず述べておきたいと思います。
1.設計工学とシミュレーション
設計工学は文字通り工学であり、工学は人間の目的を達成するための「創造」であり、何故(Why)ではなく、人間が欲する人工物やシステムをどうすれば(How)実現できるか、を追求する学問です。その成否の評価軸は有効性(実現性、効率、安全性など)です。また思考の流れでいえば、①社会的・技術的課題の把握から始まって、②モデル化という思考(機能・構造・性能について)、③有効性の確認(試作、実験、シミュレーション)という思考プロセスを辿ることになります。
現状の社会(産業界)をみると、シミュレーション全盛ともいうべき時代、あるいは人間の思惟としての本来の設計行為ではなく、AI利用も含めて、人間自身によって長年、蓄積してきた経験の成果やシミュレーション自体の結果のみに注目して設計を進める考え方に移行しつつある時代であるともいえます。敢えていえば、これらの現象は表層的な相関関係を求めているといったら言い過ぎでしょうか。
本稿では、工学は自然という大地から誕生した科学という大樹の一本のしっかりした枝であること、逆にいえば地中にしっかり根を張った科学という思考がルーツであることを確認することの重要性についてまず述べておきたいと思います。
2.自然現象の変化に規則性を見出す科学の出発点
一般にマクロ的な自然は空間的にも時間的にも常に変化する連続現象です。その自然現象の変化に規則性を見出そうとしたのが科学の出発点です。科学では、現象を「因果構造」、「メカニズム」として理解します。いいかえると、表層的な相関ではなく、「なぜそうなるのか?」(causal mechanism)を説明しようとしてきました。その際、科学は自然界の主に連続現象に注目しますが、一般に自然界の現象は複雑ですので、まずその連続現象の単純化(理想化)を行っています。卑近な例でいえば、物理では「摩擦なし」、「質点」、「剛体」などの理想化があります。ただ一方で、単純化の妥当性と再現性を検証する(どの条件で成り立つか)ことも科学の重要なプロセスです。その上で対象にした自然現象に対して、その物理法則の発見(記述)に注力し、その結果を微分方程式として表現しました。例えば、ニュートン力学(図1:第2法則)、マクスウェル方程式、シュレーディンガー方程式、流体方程式などです。
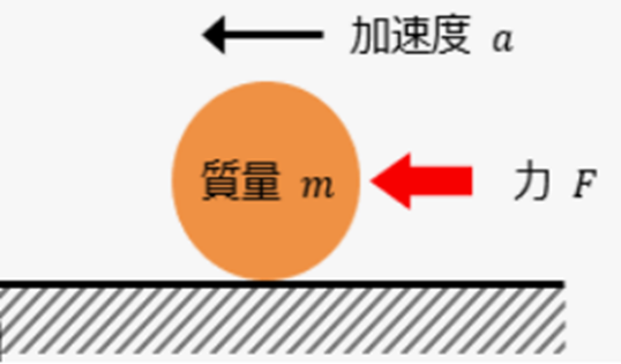
3.現象変化のプロセスの因果構造
微分方程式は、自然現象の時間的・位置的隣接点間の変化を微係数(変化率)として動的関係を表現します。言い方を変える と隣接点間の時間・空間距離の極限としての定義表現です。隣接点間の距離が近いほど厳密さに近づく。つまり変化規則を一般性(図1:第2法則)のある支配方程式として表現することになります。これは現象変化のプロセスの因果構造を示したことになります。これを現実空間の実現像として表すためには、微分方程式を解くことになりますが、現実の自然現象は「無限の空間」ではなく、特定の範囲(領域)の中で起こります。このとき、「境界での状態」(温度、速度、圧力など)を与えないと、微分方程式の解は一意に定まりません。これを境界条件(boundary condition)、または時間的な出発点としての初期条件(initial condition)と呼びます。
4.微分方程式の役割と離散化の結果
一方で、自然現象を表す支配方程式(例:熱伝導方程式、ナビエ–ストークス方程式など)は、「時間と空間のすべての点(無限の数の点)で成立する関係式」です。このことは境界条件を与えても、「解の内容」は位置と時間に関して連続的関数のままになります。言い方を変えると、境界条件を与えて空間を限定して「有限な空間内」としても、「連続無限の自由度」をもつ自然現象を対象とするということになります。しかし、現実的には無限の個数の点の情報は取り扱うことはできません。どれほど高精度・高細密な計測器が有っても空間内のすべての点を測定することはできないし、点で定義される自然現象の微分方程式を無限個の方程式として同時に解くことはどれほど優れたコンピュータでもできません。つまり解析解が存在しても計算できないことになります。また、例えば、ナビエ・ストークス方程式や弾塑性変形方程式などは、非線形性を含み、解析的に厳密な解を得ることは不可能(もしくは未知)です。したがって境界条件を与えても、「理論上の関係」は成り立つが、「具体的な値を求める(=解く)」ことは原理的に困難になります。

連続的な微分方程式 → 代数方程式の集合(有限個)
へと変換されることになります。この操作によって初めて、「有限空間内の現象を計算機で解く」ことが可能になります。計算機で解いた結果はポイント解になります。逆に、離散化して解くなら最初から差分式を作れば良いと思うかもしれません。しかし微分方程式は次の役割を持ちます。
①物理法則の表現 局所的なエネルギー保存・力のバランスの表現。
②モデルの普遍性 実験やシステムによらず原理の同一性。
③数値手法の基盤 差分法・有限要素法の導出の根拠を与えること。
④解の理論的理解 安定性・特異性・対称性の議論に使えること。
微分方程式が以上のような役割を持つが故に、「離散化」の結果としてのポイント解を中心に実務が行われることになります。その理由は、
a)現実の構造物・製品は複雑すぎて解析解が出ないこと。
b)設計では「数値解」が必要であること。
c)コンピュータとの相性がよいこと。
d)最適設計・シミュレーションに必須。
つまり最適化、耐久検証、AI設計などの流れが必須になっているからです。
しかし、離散式は「離散的近似」に過ぎず、実際の自然現象にある滑らかさ・連続性や対称性の表現が欠けるともいえますが、離散化は自然現象を計算可能な構造に変換する行為であり、「世界を理解する」からモデルを与えて、「世界を構成して扱う」科学へのシフトであるともいえます。あるいは、「微分方程式は連続世界の仮定に基づき、しかし現実に触れるのは離散的な観測と計算結果」であるともいえます。ということもあり、「世界を解析して理解する科学」から「世界をモデルとして構成して扱う科学」への変化が現に生じているともいえます。
5.科学的分析による「再現性」の保証
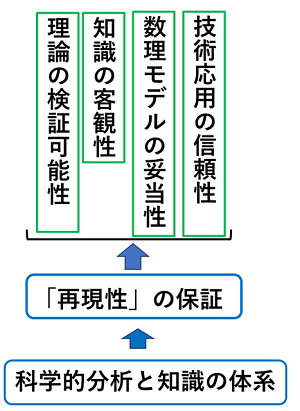
一方で、上記で述べたような科学的分析(scientific analysis)を「知識の体系」として成立させるための最も重要な条件が「再現性」の保証です。つまり「現象が個人的な経験や偶然に依存せず、客観的に確かめられる」ことを保証する性質です。再現性を必要とする項目としては、知識の客観性、理論の検証可能性、数理モデルの妥当性、技術応用の信頼性が考えられます(図3)。
近年は、以上のような経緯内容を十分に担保した分析手法として、おもに工学の様々な分野ごとのCAE(ポイント解を求めるシミュレーション(近似解析)が盛んに用いられています。これらは近似計算であるが故に、
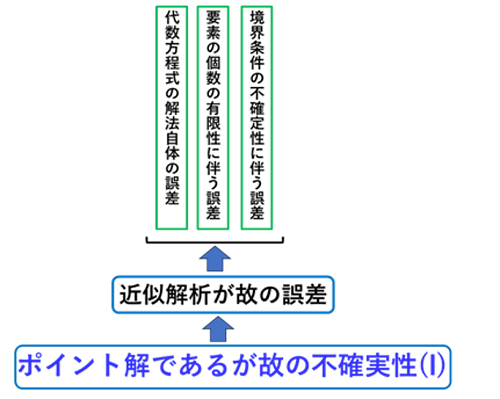
①有限自由度の代数方程式の解法自体に起因する誤差および
②シミュレーションの対象である連続空間を有限個の要素や格子に分割する際の個数の有限性に伴う誤差がある
と一般にいわれていますが、これら以外に、
③境界条件の付与の不確実性の問題もあります(図4)。
6.境界条件の不確実性に関する本質的な問題
一方、①、②の誤差に基づく不確実性よりも③の境界条件の付与の不確実性の問題のほうが実際的に問題であると指摘されています。③については、もう少し広くいえば、モデルの不確実性(いわゆる境界条件(例えば、ボルト締結部の拘束性、熱伝達係数の実測困難性、接触面の摩擦状況など)、実在材料特性(例えば、規格上の同一種のヤング率であっても固定的ではないこと)、外力条件(振動入力の周波数分布の想定困難性など)の不確実性のことをいう)ともいえます。このように境界条件不確実性に関してはいくつかの指摘はできますが、その本質的な問題は次の2点にあると思います。
逆問題の困難性:実験から境界条件を推定するのは本質的に不安定(不適切設定問題)。
感度の高さ:偏微分方程式系(特に双曲型/放物型)は境界条件に強く依存することなどの感度に関すること。
こうした観点を踏まえたうえで、境界条件の指定の重要性を考慮すべきでしょう。
7.設計における「境界条件」と「流用設計」
他方、境界条件の不確実性に関しては、日本のモノづくり(製造業)の歴史の中で、現状、流用設計が多用されていることにも関係すると思われます。つまり「流用設計」と「境界条件」は、設計における「適用範囲の正しさ」という共通の課題を表しています。
流用設計とは、いうまでもなく既存製品の設計(形状・材料・構造・条件・モジュールなど)を新しい用途や条件に再利用する設計手法のことです。流用に当たって、「境界条件が未知な状態での設計探索が常態化している」という現象も指摘されていて、こうした常態化は、まさに流用設計や設計自動化(CAE・AI設計)の実際の現場で多く見られるともいわれる、ある種、構造的問題でもあります。例えば、プラットフォーム共通化に伴う自動車部品設計、筐体構造の流用に伴う家電・電子機器設計、派生設計の多い航空宇宙構造設計、現場ごとに荷重条件・支持条件が変わる建設・プラント設計などの分野における指摘もあります。
原因としては、開発期間の短縮、システム間の分業化、CAEのブラックボックス化、サロゲートモデル/AI設計の誤用などが考えられますが、結果的に科学的再現性を失った広い意味での設計(非)最適化が行われた結果なのでしょう。あるいはポイント解をベースにした設計の宿命なのでしょうか。

最適化/機械学習による設計空間探索ソフトウエア pSeven Desktop
pSeven Desktopであらゆる設計リードタイムを短縮。煩わしい作業を削減し、CAD・CAE・データとプロセスを自動化します。pSeven Desktop独自のAIと強力な自動化エンジンによって、最適な設計条件を効率的に発見が可能です。

設計最適化と自動化を実現する革新的なエンタープライズ基盤 pSeven Enterprise
設計プロセスの自動化・最適化、モデル・ワークフローの統合と展開を目的としたエンタープライズ向けのデータ活用プラットフォームです。設計者やエンジニアが組織を横断し、複合領域の複雑な課題を解決するために、最適化技術、機械学習モデル・シミュレーションモデルの統合、ノーコードアプリの活用を支援します。
